Financiële functies van excel (met voorbeelden)
1. VF-functie
De FV-functie retourneert de toekomstige waarde van een investering met behulp van constante betalingen en een constant rentepercentage. In eenvoudige bewoordingen levert het een toekomstige waarde van een belegging op waarbij u gedurende de gehele beleggingsperiode constante betalingen en een constant rentepercentage heeft.
Syntaxis
FV(tarief,nper,pmt,[pv],[type])
Argumenten
- rente: een constant rentepercentage dat u wilt gebruiken in de berekening.
- nper: aantal betalingen.
- pmt: een constant betalingsbedrag dat periodiek moet worden betaald gedurende de looptijd van de belegging.
- [pv]: De contante waarde van toekomstige betalingen. Het moet als een negatieve waarde worden ingevoerd. 0 indien weggelaten.
- [type]: een getal dat aangeeft wanneer de betaling verschuldigd is. 0 = aan het einde van de periode, 1 = aan het begin van de periode.
Opmerkingen
- Als pmt het geld is dat u heeft betaald (bijvoorbeeld spaardeposito’s etc.), moet de waarde negatief zijn; en als het ontvangen geld betreft (inkomsten, dividenden), moet de waarde positief zijn.
- Zorg ervoor dat u een consistent gespecificeerd tarief en aantal betalingen hanteert. Als het tarief op jaarbasis is, moet u ook de betalingstermijnen op jaarbasis opgeven en als u de betalingen op maandbasis wilt opgeven, moet u het rentepercentage omrekenen naar een maandbasis door te delen door 12. Hetzelfde geldt voor een kwartaalbedrag. en halfjaarlijks.
Voorbeeld
In het onderstaande voorbeeld hebben we een rentepercentage van 10%, 5 betalingen op jaarbasis, een betalingsbedrag van $ 1.000, geen PV-bedrag en betalingstype aan het begin van de periode gebruikt. En de functie heeft 6716 geretourneerd in het resultaat.
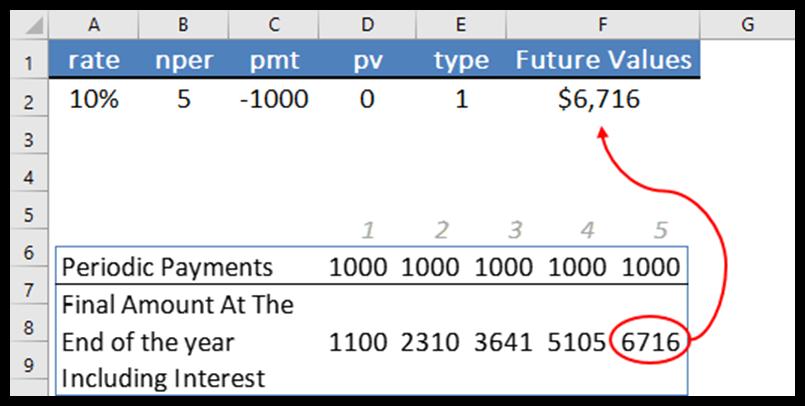
Laat me de verschijnselen achter FV uitleggen.
Aan het begin van elke periode berekent zij de rente over de betaling en draagt dit bedrag (werkelijk bedrag + rente) over naar de volgende periode. En in de volgende periode zal dezelfde berekening worden gemaakt, enzovoort.
Het beste van FV is dat het deze stapsgewijze berekening voor u in één cel kan uitvoeren. In het onderstaande voorbeeld hebben we gebruik gemaakt van maandelijkse betalingen.
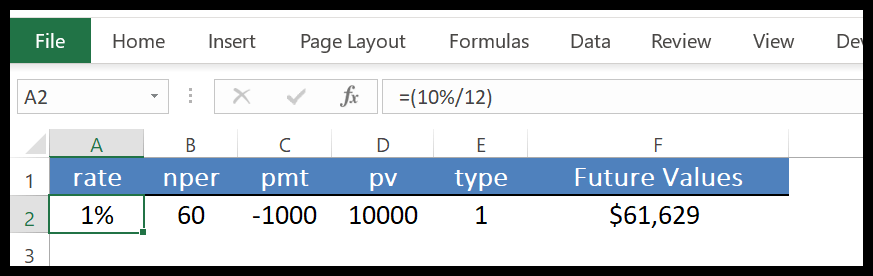
Hiervoor hebben we de jaarlijkse rente omgerekend naar één maand door te delen door 12 en 60 maanden in plaats van 5 jaar en vervolgens 10.000 opgegeven als afbetaling. Met FV kunt u ook samengestelde rente berekenen .
2.EMP
De PMT-functie retourneert een periodieke leningbetaling die u moet betalen. Simpel gezegd berekent het de terugbetaling van de lening op basis van vaste maandelijkse betalingen en een constant rentepercentage (betaling van de lening op basis van vaste maandelijkse betalingen en een constant rentepercentage).
Syntaxis
PMT(tarief, aantal, pv, [fv], [type])
Argumenten
- rente: het rentepercentage van de lening. Deze rente moet constant zijn.
- nper: Het totale aantal betalingen.
- pv: De huidige waarde of het totale bedrag van de lening.
- [fv]: De gewenste toekomstige waarde of kassaldo na de laatste betaling. De standaardwaarde is 0.
- [type]: Gebruik 0 of 1 om de vervaldatum van de betaling op te geven. U kunt 0 gebruiken als de betaling aan het einde van elke betaling moet plaatsvinden, of 1 als de betaling aan het begin van elke periode moet plaatsvinden. Als u het type niet opgeeft, wordt ervan uitgegaan dat het 0 is.
Opmerkingen
- Het PMT-betalingsretourbedrag omvat alleen betalingen en rente, maar exclusief belastingen en andere leninggerelateerde kosten.
- U moet zeker zijn wanneer u de waarde van de argumenten rate en nper opgeeft. Als u maandelijkse betalingen wilt betalen voor een lening met een looptijd van vijf jaar tegen een jaarlijkse rente van 8%, gebruikt u 8%/12 voor rente en 5*12 voor nper. Voor jaarlijkse betalingen op dezelfde lening gebruikt u 8% voor het tarief en 5 voor het aantal.
Voorbeeld
Stel dat u een hypotheek met een looptijd van 20 jaar wilt afsluiten voor € 250.000, uitgaande van een rentepercentage van 2,5%. Nu kunnen we PMT gebruiken om uw maandelijkse betalingen te berekenen.
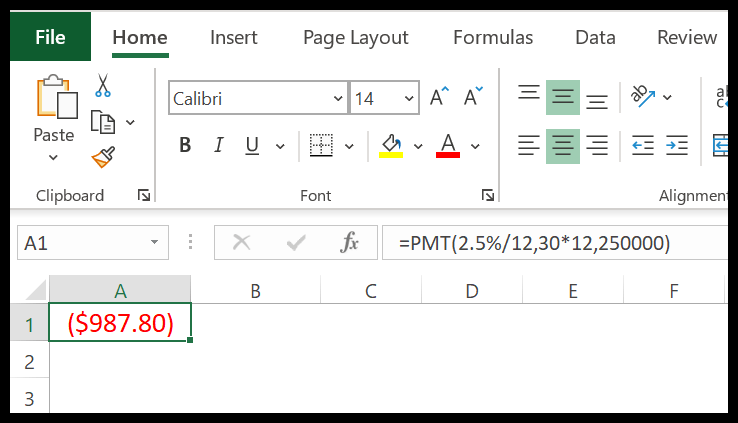
In de bovenstaande berekening hebben we de jaarlijkse rente omgerekend naar maanden door te delen door 12 en de jaren naar maanden door te vermenigvuldigen met 12.
Maar we hebben geen toekomstige waarde genoemd en het betalingstype is standaard. Het resultaat is dus dat we een negatieve waarde hebben, omdat het bedrag van $987,80 het bedrag is dat we 30 jaar lang elke maand moeten betalen.
3. PV
De PV-functie retourneert de huidige waarde van een financiële investering of lening. Simpel gezegd: met de PV-functie kunt u de huidige waarde van een investering of lening berekenen, waarbij u kunt controleren of deze aanwezig is.
Syntaxis
PV(tarief, aantal, pmt, [fv], [type])
Argumenten
- rente: Het rentepercentage voor het terugbetalen van de lening.
- nper: totaal aantal betalingstermijnen
- pmt: Een constant bedrag dat u na elke periode moet betalen.
- [FV]: De toekomstige waarde of kassaldo van een lening of investering die u na de laatste betaling wilt bereiken. Indien dit wordt weggelaten, wordt ervan uitgegaan dat het 0 is.
- [type]: Tijdstip van betaling. Begin van de periode (gebruik “0”) of einde van de periode (gebruik “1”).
Opmerkingen
- De eenheden die u als argumenten gebruikt, moeten consistent zijn. Als u bijvoorbeeld periodes in maanden gebruikt (36 maanden = 3 jaar), moet u de jaarlijkse rente omrekenen naar een maandelijkse rente (6%/12 = 0,5%).
- De PV-functie is een annuïteitenfunctie. In lijfrentefuncties worden contante betalingen die u doet, weergegeven door negatieve getallen en worden betalingen die u ontvangt weergegeven door positieve getallen.
Voorbeeld
Stel dat u € 4.000,- in een investeringsplan wilt investeren en dat u in ruil daarvoor aan het eind van elk jaar € 1.000,- ontvangt gedurende de komende vijf jaar.
Dit betekent dat u de komende vijf jaar in totaal € 5.000,- krijgt.
Het punt is nu dat u moet evalueren of deze investering winstgevend is of niet. U investeert vandaag € 4.000,- en het rendement zal u binnen de komende vijf jaar ten deel vallen.
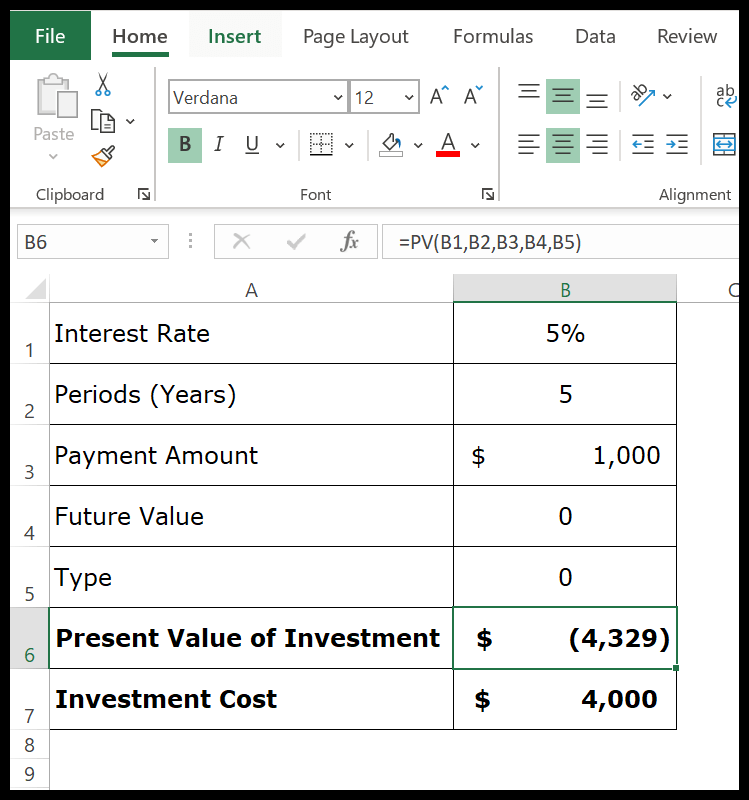
In de bovenstaande berekening werd -4329 geretourneerd. De huidige waarde van uw belegging is € 4.329 en u investeert er € 4.000 in. Uw investering is dus rendabel.